Phase-Based Ranging vs. Round-Trip CIR

Wireless ranging technologies are critical for applications that require precise distance measurements, such as indoor navigation, asset tracking, and industrial automation. Among the methods available for distance estimation, Phase-Based Ranging (PBR) has been referenced in Bluetooth SIG collateral material as an example of how distance calculation could be performed using the Bluetooth® 6.0 Channel Sounding feature. However, while PBR offers a good starting point, there are significant limitations, especially when compared to more advanced approaches, such as Round-Trip Channel Impulse Response (CIR) calculation which is enabled by Metirionic’s Pathfinder algorithm.

In this article, we’ll compare PBR and Round-Trip CIR, explaining why Pathfinder provides a more accurate and reliable solution for ranging.

What Is Phase-Based Ranging (PBR)?

Phase-Based Ranging (PBR) uses the phase difference between two signals transmitted at different frequencies to estimate the distance between two devices. The phase shift of these signals is related to the time delay of the signal, which corresponds to the distance.

While PBR is useful in certain scenarios, it is important to note that the Bluetooth 6.0 specification does not define a specific algorithm for calculating distances. PBR is mentioned in Bluetooth SIG material as one example of how developers might use Channel Sounding data to estimate distance. However, the actual algorithm is outside the scope of the specification and left to developers to implement, providing maximum flexibility for innovation and differentiation.

Limitations of PBR: Multipath Propagation

One of the main challenges with PBR is its sensitivity to multipath propagation—where signals reflect off objects and surfaces, creating multiple paths that can interfere with the direct signal. In PBR, only the phase difference is used to estimate distance, and the method does not have a mechanism to reliably distinguish between the direct path and reflected paths.

This leads to inaccuracies in complex environments, where multiple signals arrive at different times, combining in ways that distort the phase measurements or cancel it out alltogether. Metirionic’s previous tests showed that while PBR could achieve cm-level precision in limited controlled environments, the errors grew significantly—up to several meters—when tested in environments with high levels of multipath interference such as indoor and even in certain outdoor scenarios.

Round-Trip CIR: A More Comprehensive Approach

The limitations of PBR highlight the need for a more robust method of distance measurement. Unlike PBR, which relies solely on phase differences, Round-Trip CIR uses the complex representation of the received signal vectors, incorporating both in-phase (I) and quadrature (Q) components of the signal to calculate the CIR. This provides a more detailed and accurate representation of how the signal interacts with the environment.

By analyzing the entire CIR—the signal’s behavior on both the forward and return trips—one can gain a much clearer picture of the environment. The Round-Trip CIR accounts for not just the phase differences but also the magnitude of the signal, providing a more reliable estimate of the distance, even in environments with significant reflections and scattering.

The Relationship Between I/Q Values and Phase and Magnitude

To understand why Round-Trip CIR is more accurate than PBR, it’s important to recognize the relationship between the I/Q values of the received signal and its phase and magnitude. The I/Q components represent the signal in a complex plane, where the I (in-phase) component corresponds to the real part of the signal, and the Q (quadrature) component corresponds to the imaginary part.

• The magnitude of the signal is determined by the distance from the origin to the signal point in the I/Q plane, calculated as $$\text{Magnitude} = \sqrt{I^2 + Q^2}$$
• The phase of the signal is the angle formed between the signal point and the I-axis, calculated as $$\text{Phase} = \arctan\left(\frac{Q}{I}\right)$$.

While PBR uses only the phase information to estimate distance, the CIR method takes both phase and magnitude into account. By doing so, it provides a more comprehensive understanding of how the signal is affected by the environment, leading to greater accuracy, particularly in multipath scenarios.

The Difference between PBR and Pathfinder with Round-Trip CIR

Metirionic’s Pathfinder algorithm takes full advantage of the Round-Trip CIR, allowing it to outperform PBR in environments with significant multipath propagation. Here’s why Pathfinder offers a superior solution:

1. Comprehensive Signal Analysis: By analyzing both the phase and magnitude of the received signal vectors (I and Q values), Pathfinder gets a complete picture of the signal’s behavior. This leads to more accurate distance estimates, even in challenging environments.
2. Multipath Mitigation: Pathfinder is specifically designed to manage multipath propagation. By analyzing the full CIR, including reflections and scattered signals, it can separate the direct path from reflected paths, ensuring that the distance measurement is based on the true signal travel time.
3. Greater Accuracy in Real-World Tests: In cable car tests on an 11.5-meter track, PBR showed significant errors due to multipath effects, with deviations of up to 6 meters in some instances. When the Pathfinder algorithm was applied, the Round-Trip CIR delivered a constant cm-level accuracy across the track, demonstrating its ability to handle real-world indoor conditions.
4. Consistency Across Environments: One of Pathfinder’s key advantages is its consistency. Whether in a clear line-of-sight environment or a reflective, obstacle-filled space, Pathfinder’s ability to analyze the full CIR ensures reliable, precise distance measurements.

To illustrate the differences in accuracy between PBR and Pathfinder with Round-Trip CIR, consider the following figures:

Figure 1 visualizes the cumulative distribution function (CDF) for PBR of these errors. The x-axis represents the error (in meters), and the y-axis indicates the probability. The orange line at one standard deviation (one sigma) shows that 68% of errors were below 1.75 meters. The green line, representing two standard deviations (two sigma), illustrates that 95% of errors were within 4 meters.

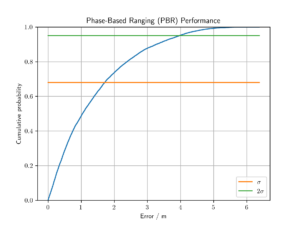
Figure 1: Cumulative Distribution Function (CDF) of PBR Errors.

Figure 2 visualizes the cumulative distribution function (CDF) for MARS Pathfinder utilizing Round-Trip CIR of these errors. The x-axis represents the error (in meters), and the y-axis indicates the probability. The orange line at one standard deviation (one sigma) shows that 68% of errors were below 1 meter. The green line, representing two standard deviations (two sigma), illustrates that 95% of errors were within 3 meters.

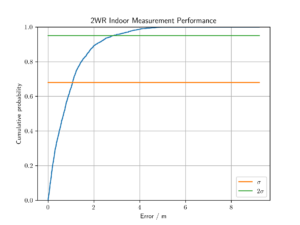
Figure 2: Cumulative Distribution Function (CDF) of Pathfinder with Round-Trip CIR Errors.

These figures clearly demonstrate that Pathfinder with Round-Trip CIR significantly reduces errors compared to PBR, providing more accurate and reliable distance measurements across various environments.

Looking Ahead: The Future of Bluetooth Channel Sounding

While the Bluetooth 6.0 specification with Channel Sounding does not include a specific algorithm for distance calculation, it has already laid the groundwork for significant improvements in accuracy compared to older methods like RSSI-based ranging. In turn, new use cases and applications will emerge that take full advantage of such secure, fine ranging, and will naturally encourage ongoing improvement. The Bluetooth 6.0 specification specifies that each measurement within the “Time for Phase Measurement” (T_PM) results in a single Phase Correlation Term (PCT) value expressed as a complex number I+jQ. The IQ terms are each encoded using 12 bits. This opens the door for advanced algorithms, like Pathfinder, to be implemented on top of the standard, providing even more precise distance measurements by utilizing these complex signal representations.

Looking forward, there’s potential for future specification versions to support additional features, such as one-way ranging (1WR), which would further enhance distance calculation capabilities. However, even today, the combination of 2-way ranging (2WR) with Pathfinder already provides a solid foundation for achieving highly accurate distance measurements in a variety of environments.

Conclusion

While Phase-Based Ranging (PBR) offers a simple method for distance measurement in some limited scenarios, its limitations in handling multipath propagation make it less reliable for high-precision applications especially in real-world conditions. By using the complex representation of the received signal vectors (I and Q values), Metirionic’s Pathfinder algorithm offers a more comprehensive and accurate approach, based on Round-Trip CIR, and is able to do so while minimizing computations and thus conserving power. This allows for consistent cm-level precision, even in environments where PBR struggles. As Bluetooth Channel Sounding evolves, Pathfinder continues to push the boundaries of what’s possible in wireless ranging.